Gentle Math for Meditators: Vibration

With lots of animations and zero equations

Math and meditation make a strange pair.

You might even see them as opposites: mathematics requires deep concentration on abstract concepts; meditation involves relaxing attention¹ and letting go of concepts.

But mathematics is unreasonably effective at describing the physical world. So maybe it can help us describe mental world as well.

In particular, the language of vibration—of circles, cycles, frequencies, waves, phases, oscillation—comes up constantly when talking about states of consciousness. It’s almost cliche in New Age literature, with practitioners claiming “everything is vibration” or trying to “raise their frequency”.

But all that nonsense comes from an intuitive wellspring: vibration underpins everything, and our minds are no exception.

(I’'ll also recommend Sabine’s Substack, Science without the Gobbledygook, which is the most delightfully German way to say Minus the Nonsense I can imagine)

Outline

• Going in Circles

• Everything is Vibration

• The Shape of Waves

• A Recipe for Anything

• I Am a Strange Loop

Going in Circles

I promised “gentle math” in the title, so let’s start simple. And what could be simpler than a circle?

Pick out a center point, then put a dot at every place exactly one inch from there.² Boom, you’ve got a circle.

When we talk about circular motion, the terminology changes a bit. We tend to speak of waves, oscillation, or vibration. These words describe anything that wiggles back and forth around a center point—similar to how our circle above is cycling around a center point. The difference is that while a circle moves in two dimensions, waves move in one dimension.

In fact, if we break things down a bit, our 2D circle above is really made up out of two waves, one moving vertically and one horizontally:

A dot moves in a circle. The top wave tracks the horizontal position of the dot, and the right wave tracks the vertical position.

(If the sudden appearance of sine waves is triggering PTSD from high school math—relax! We won’t get into trigonometry here.)

You can think of waves as one-dimensional circles, or of circles as two-dimensional waves. So I’d argue that waves are even simpler than circles—they just describe anything that wiggles, anything that moves back and forth around a center.

Bounceback Systems

Nothing rests; everything moves; everything vibrates.

—The Kybalion

I like to call anything that wiggles like this a bounceback system. Some examples:

• A playground swing

• Your lungs as they breathe in and out

• A flag flapping in the wind

• The shock absorbers on a car or bike

• The keys on your computer keyboard

• Your vocal chords

But if this were a physics textbook, we’d probably be talking about pendulums:

Bounceback systems have a happy resting spot, like the pendulum when it’s pointed straight down. But if you disturb them a bit, they start to wiggle back and forth around that happy spot, rather than falling straight back into it and resting there.

If we plot the position of our pendulum over time, we get a wave like the ones above:

Note that we’ve flipped things sideways here: the pendulum is the dot moving up and down on the left.

In the real world, our pendulum would eventually run out of energy³ and rest back in the vertical position. But if there weren’t any wind or friction to slow it down, it’d keep wiggling back and forth forever!

There’s a simple way to state the dynamic at play here: a bounceback system accelerates back towards its stable point, in proportion to how far away it is. Push the pendulum a little, it accelerates back just a little; push the pendulum a lot, and it’ll pick up real speed.

But no matter how far you push it, it’ll always overshoot, past its happy spot at the bottom. At that point, it starts to accelerate in the opposite direction, triggering an infinite loop.

Everything is Vibration

So why is this useful knowledge for meditators? The key insight is that everything you experience is vibratory. Bounceback systems are everywhere.

Sound is the most obvious example—vibrations in the air wiggle your eardrums, and you experience a voice, a song, applause. And sine waves, like the ones we explored above above, make the simplest conceivable sound—a tiny hum. Here’s one that wiggles 440 times per second:

Vision is a bit harder to think of in terms of vibration, but every photon that hits your eyes is vibrating⁴ trillions of times per second. The only difference between yellow and blue is that blue is vibrating a bit faster. And if you pay close attention to your visual field (especially with eyes closed), you’ll notice a whole lot of flickering and pulsing. In fact, the image on the screen in front of you is flickering somewhere between 60 and 250 times per second—so fast your brain can’t see it.

The electromagnetic spectrum, with the small visible part highlighted in the center

Even smell and taste are hypothesized to be vibratory phenomena, related to how chemicals wiggle after attaching to the chemoreceptors in your nose and tongue. Chemicals with the exact same shape but different weights (e.g. water with an extra neutron) wiggle differently, causing a difference in taste.

Really everything about the nervous system is vibratory: different neurons are described as having different vibrational frequencies; EEG, one of our best windows into brain activity, measures electromagnetic vibrations emanating from the brain, with different frequencies roughly corresponding to different conscious states:

And at the macro scale, any repetitive behavior—like breathing, shivering, blinking, walking, stirring, or brushing—can be characterized in terms of vibration.

So developing a more intimate understanding of vibration gives us a better vocabulary for describing and modulating our experience.

The Shape of Waves

Some of these sensations, like breathing, follow the nice smooth curve of a sine wave. But most of them take on stranger shapes, with complicated rhythms and sudden jumps.

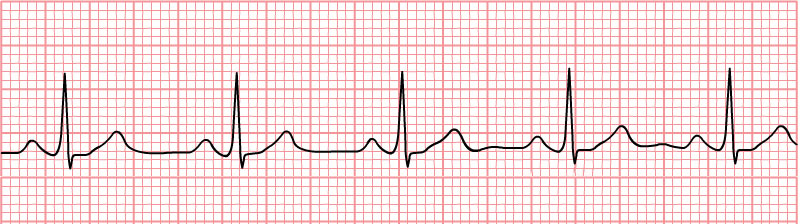
Consider your heartbeat:

It has the regular peaks and valleys of the sine wave, but the peaks are sharp and sudden, while the valleys are flat and extended. And there seem to be a few signals mixed together here, with some smaller peaks surrounding the main peaks.

There are a few basic wave shapes (which will be particularly familiar to electronic musicians) that come up frequently:

The sine wave has nice smooth acceleration and deceleration; the square wave jumps suddenly between two extremes; the triangle wave keeps a constant speed, but jerks a bit when it has to reverse direction; the sawtooth combines the triangle and square waves, with a constant speed that suddenly jumps back to the opposite extreme

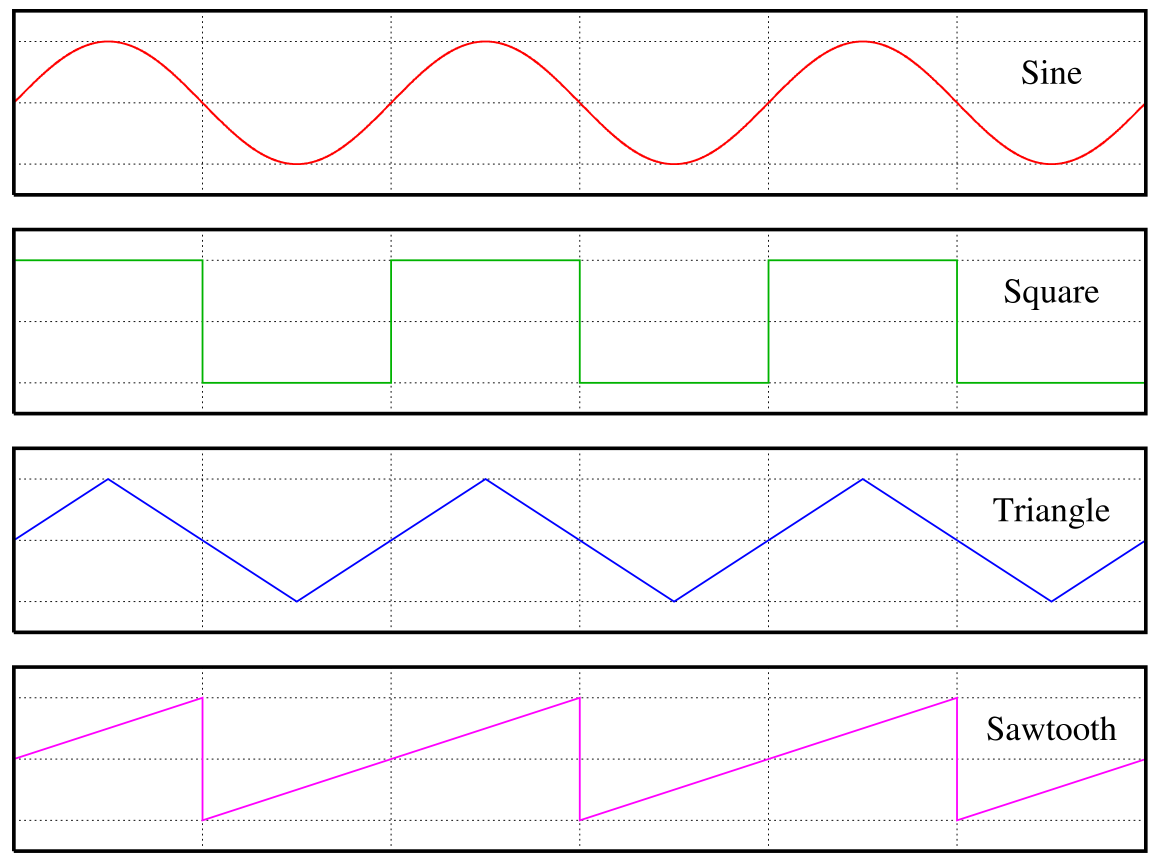
And we can get all sorts of interesting shapes by adding different waves together:

The red wave is just the blue and the green wave, added together. If you played the red wave as a sound, you’d hear two different notes, like pressing two piano keys at the same time

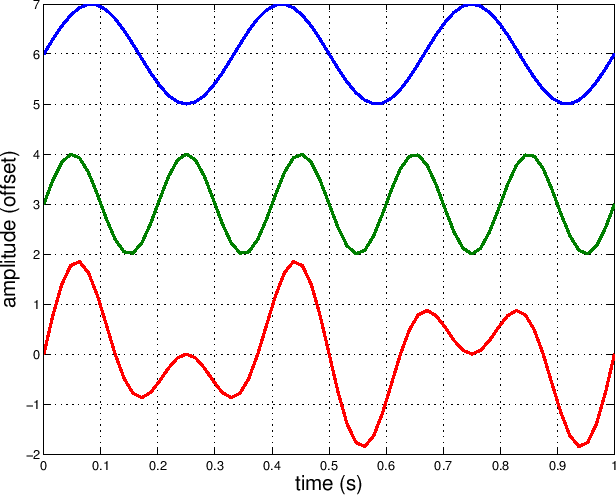
So vibration doesn’t just cover the smooth in-and-out motion of a pendulum or your breath. Flapping, twisting, throbbing, jiggling, bouncing, heaving, winding, rocking, quivering—all these types of motion can be captured by the mathematics of vibration.

A Recipe for Anything

In fact, we can make any⁵ shape we want by combining sine waves (or, in 2D, spinning circles).

More on this animation below. Found via r/interestingasfuck. If you know the original source, leave a comment and I’ll give credit.

There are three numbers we care about when combining waves (or spinning circles) to create a recipe⁶ for something bigger:

• The amplitude: how high are the peaks and how low are the valleys? or, how big is the circle?

• The frequency: how many wave peaks occur each second? or, how quickly is the circle spinning?

• The phase: does the wave start at a peak, a valley, or somewhere in between? or, which direction is the circle pointed when the spinning starts?

In our “recipe” analogy, the ingredients are frequencies, and the amount of each ingredient is the amplitude. The phase might be the timing of when each ingredient is added—the analogy breaks a bit here. (And in many cases, like with sound waves, the phase doesn’t matter at all.)

For example, you can build a square wave out of sine waves with increasingly higher frequencies:

Each frame adds another sine wave to the green signal, with increasingly higher frequencies. We’d need to add an infinite number of them to get a perfect square wave.

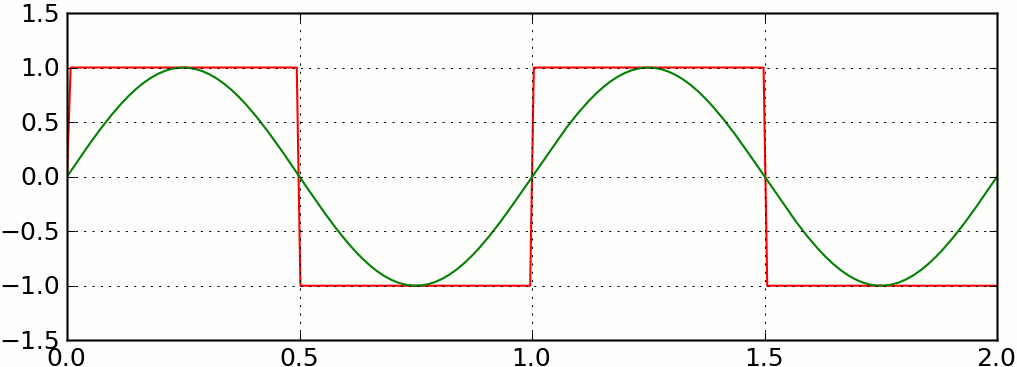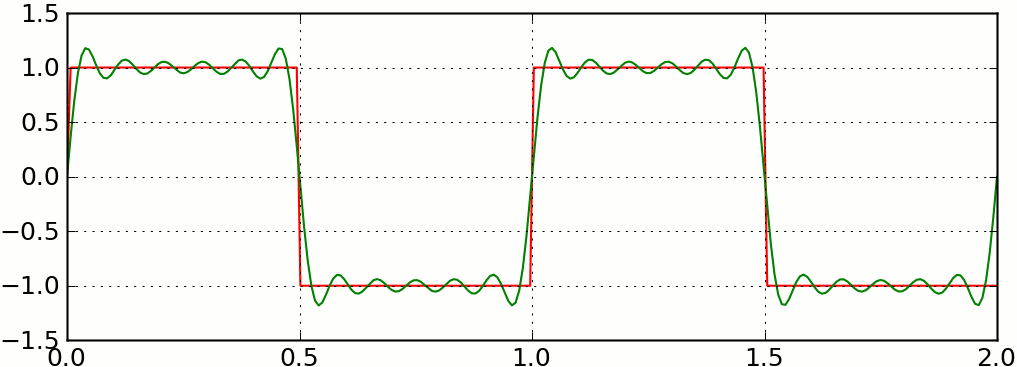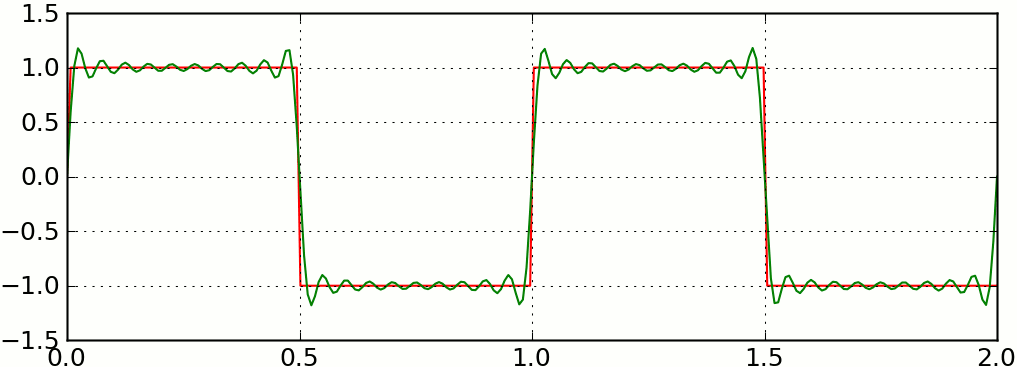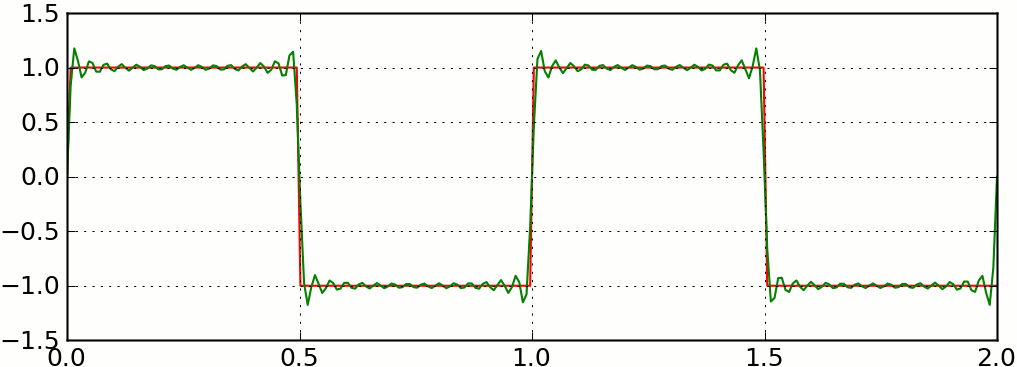
We can lay this out in 2D as well, just by replacing waves with spinning circles. We add them together by stacking the circles on top of each other, putting each circle’s midpoint somewhere (the phase) along the edge of the previous circle.

And then we press play:

Each row shows in this animation shows what happens when we add one more spinning circle to the mix. Note how the black dots in the middle column get closer and closer to tracing out a (very wobbly) 2D square. And when we plot the vertical position of those dots in the right column, we get closer and closer to our 1D square wave.

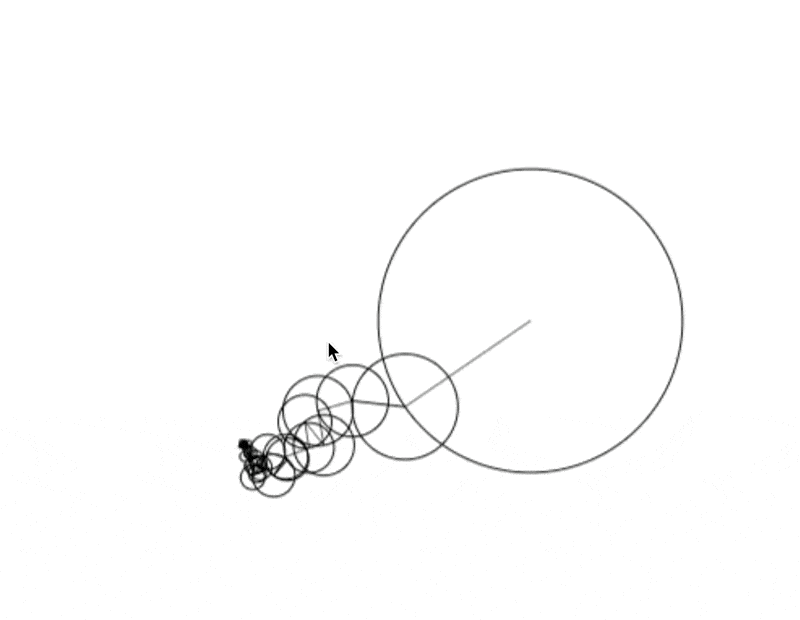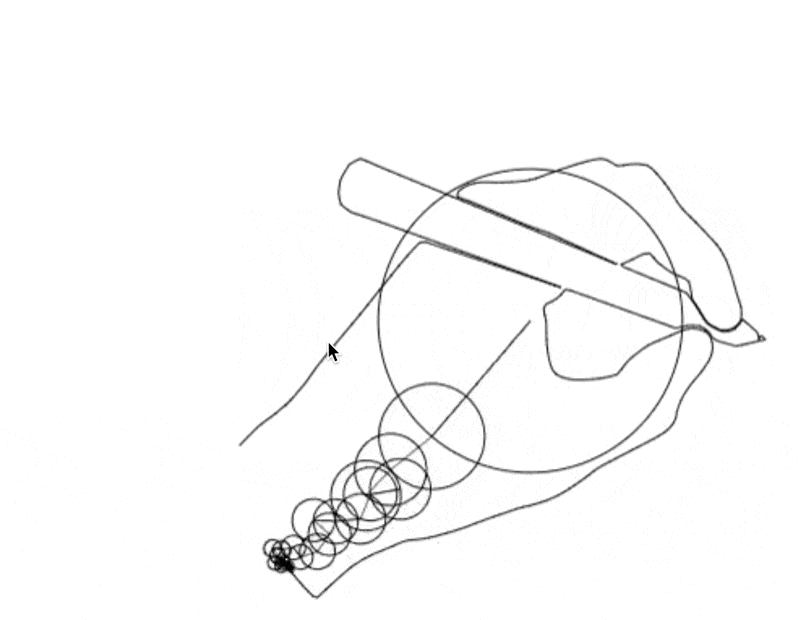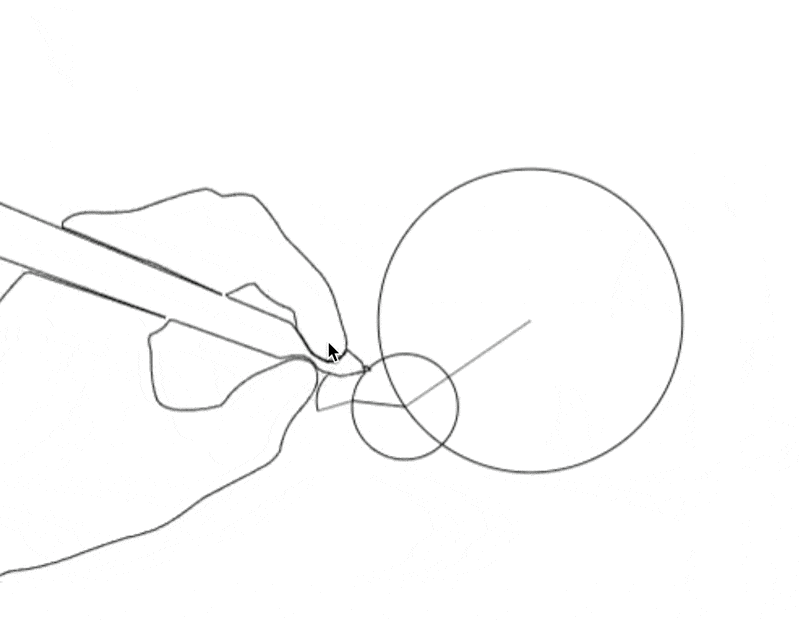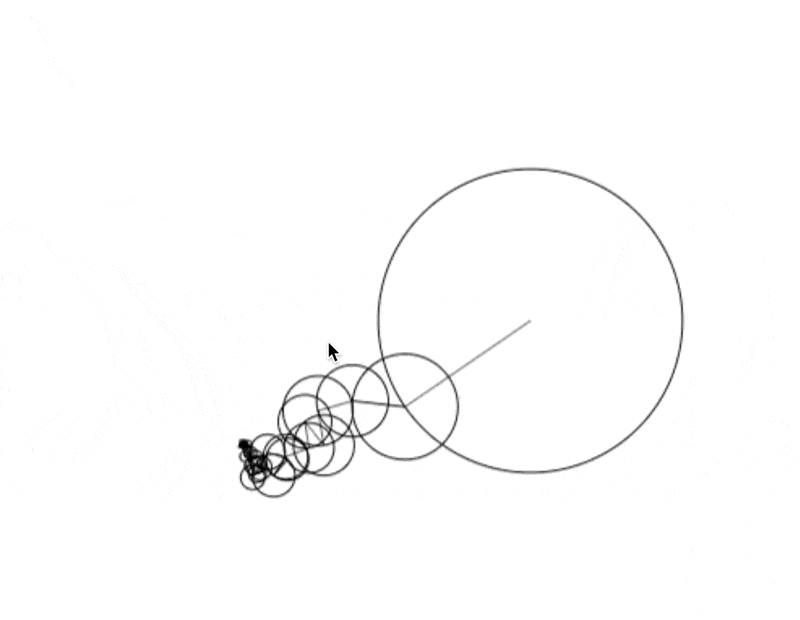
But it’s not just squares—any loop, no matter how complicated, is made up of spinning circles! That’s how we get our drawing of a hand: we just stack spinning circles, with very precise frequencies, amplitudes, and phases.

The recipe above has dozens of spinning circles, each with its own frequency, amplitude, and phase. It’s perfectly calibrated to produce a line drawing of a hand holding a pen. A similar recipe exists for any⁷ line drawing you can think of.

I Am a Strange Loop

When sitting in meditation, I’m often struck by the fact that the gestalt of my experience—the sum of all my thoughts, emotions, and sensations—is exactly like the hand drawing above. My state of mind is composed of many different vibrations, all added together into something that seems much more intricate.

Take, for instance, your internal monologue (assuming you have one): like any sound, hallucinated or heard, it’s just a vibration. It’s made up of a handful⁸ of waves added together.

Scientifically-minded meditators often describe their experiences in terms of vibration. I wrote the following in Macro and Microphenomenology:

Some contemporary microphenomenologists are even helping to translate traditional meditative concepts into contemporary scientific terms: Romeo Stevens has observed that most of the mental events the Buddha discusses occur very rapidly, in the 10-40 Hz range; Nick Cammarata and Daniel Ingram concur, claiming that tanha specifically occurs between 25 and 100 milliseconds after a stimulus (which translates precisely to 10-40 Hz!).

Another data point: I’ve heard Roger Thisdell say that he gained insight into centerlessness after noticing his sense of center would reassert itself at a rate of about 1.6 Hz.

Thinking in terms of vibration helps me break down my experience into its component parts. I can feel anxiety as a twisting in my stomach, sometimes in combination with a throbbing between my temples. Panic is a sudden increase in both the frequency and amplitude of those sensations. And recognizing this is a huge help in mitigating the effects—often I just need to relax the muscles in my abdomen, and any anxiety dissipates.

As I deepen my meditation practice, I can increasingly see the individual vibrations making up my experience, and even start to bring them into harmony. The throbbing in my temple is accompanied by a flashing white spot in the corner of my vision; the ringing in my ears syncs up with the visual snow behind my eyelids; the sound of a churning dishwasher is connected to an eddy of tactile sensation in my torso. These synesthetic harmonies are usually quite enjoyable.

Things get even more pleasant when the vibrations dissolve into white noise. Some of the deeper experiences I’ve had resemble a field of evenly distributed tingling, buzzing, or static. And importantly—as an exploration of the math will tell you—the recipe for white noise is a combination of every frequency, in roughly equal amounts. Everything, everywhere, all at once.

---

---

If you’re mathematically inclined, there are a ton of great courses out there on vibration. None is better than Prof. Brad Osgood’s course on the Fourier Transform. His awe at the beauty of oscillation is infectious.

If you’re more a hands-on kind of person, I love playing with audio synthesis to explore the dynamics of vibration. VCV Rack is a wildly fun (and free!) program for making strange sounds and beautiful music with nothing but vibes.

But all you really need to do is open your eyes. As I sit here typing, I can hear music behind me; my fingers hit the keyboard in time with the beat; the pothos plant next to me wiggles with each keystroke.

Bounceback systems are everywhere.

1. Some practices involve focusing your attention, typically fixating it on a single object. I’ve argued before that these practices are a prelude to learning how to relax attention, which gives rise to the subtler and more beautiful meditative states.

2. The formal definition of a circle is “the set of all points in a plane that are at an equal distance (called the radius) from a fixed point (called the center).”

3. The technical term for this is “damping”. You can also have the opposite effect, “driving”, where some force pushes the pendulum higher and higher with each swing.

4. The way light vibrates is a bit different from how sound vibrates—it’s not really a vibration in 3D space, but a vibration in the electromagnetic field. But some popular physical theories like Kaluza-Klein reconceptualize the electromagnetic field as a fourth tiny spatial dimension!

5. Approximately. Some things you might want to draw wouldn’t really count as “shapes” (e.g. a bunch of randomly placed dots). The shape has to form a closed loop. And some shapes (e.g. those with sharp corners) might require an infinite number of ingredients.

6. The technical term for this is Fourier Analysis. The Fourier Transform allows us to convert back and forth between the recipe (the frequency domain) and the signal generated by the recipe (the time domain).

7. See footnote 5.

8. Some back of the envelope math with Claude suggests you only need about 100 frequencies—100 individual sine waves—to reliably represent speech.