Note: I wrote this piece before the announcement of Drake’s passing. His equation was a major inspiration for me as an early teen, and he’ll be missed.
The Drake Equation is a famous attempt to quantify the probability of humanity seeing another technological civilization. It has its flaws, but most alternatives consist only of slight modifications.
Let’s see if we can come at the problem from another angle.
Outline
The Drake Equation
Overview
The Drake Equation quantifies the number of civilizations N in our galaxy that we stand a chance of communicating with. Here’s a simplified version:
N = R * n * F * LWhere:
Ris the average rate of star formationn is the average number of planets per star that might support life
Fis the fraction of viable planets where intelligent life actually grows at some pointLis the average lifetime of technological civilizations
The original Drake Equation has some more intermediate terms, but you get the idea.
Interpretations
Results for N vary widely based on assumptions made about the individual parameters.
Astronomy has led to fairly accurate determination of some values: we know R (the rate of star formation) is about 1.5-3 stars per year, and some basic assumptions about habitability put n (the number of habitable planets per star) at about .4.
L, the average lifetime of a technological civilization, is an interesting value, which we at least have a little data for: humanity has so far lasted a century or so as a technological species. Low values for L are effectively predictions that humanity will exterminate itself (e.g. through nuclear war or climate disaster) before we become interplanetary.
But the value of F—the fraction of habitable planets that go on to develop intelligent life—is anyone’s guess. We have only one datapoint: Earth. This hasn’t stopped scientists from trying though—some have tried to extrapolate its values from the evolutionary timeline on Earth or the apparent lack of a second abiogenesis. Estimates range from tiny fractions small to nearly 100%.
An Alternative Approach
Rather than trying to estimate F from limited data, we can turn the question around a bit: given a particular probability of life evolving around a star, what are the odds we’d be the only ones here? I.e. how likely is it that intelligent life evolved exactly once within our galaxy, or within the Universe as a whole?
It’s fairly straightforward to calculate the expected number of civilizations given a certain probability of life evolving around a star. We can think of a large k-sided die—if the die lands on 1, you get life; any other value yields nothing. Then we just have to roll the die once for each star.
A Coin Flip
To start with an easy example, let’s use a coin (i.e. a 2-sided die). If we flip the coin S times, what are the odds we only get a single Heads?
Working manually:
S=1 → 50% (it will either land Heads or Tails)
S=2 → 50% (HT and TH work, out of the 4 possible combinations)
S=3 → 37.5% (HTT, THT, or TTH out of the 12 possible combinations)
In general, there are 2^S possible flip sequences, and there are S ways to get exactly one Heads (in the first spot, the second spot, …or the Sth spot). So the general formula is
P = S/2^SI.e. if we flip a coin S times, we can expect to get exactly one Heads with probability S/2^S.
We know there are about 100 billion stars in the Milky Way, or about 2^26. Plug that in for S and we get
P = 2^26 / 2^(2^26)
= 1 / 2^ (2^26 - 26)where P is the probability we’d find ourselves alone.
This is such an outrageously tiny number I can’t find a calculator that will handle it. Suffice it to say, if there were 50/50 odds of life evolving around a given star, the Milky Way would be teeming with life (about 50 billion civilizations!)
Lowering the Odds
But the emergence of life around a star is probably a rarer event than that. What happens if we increase the number of sides on our die?
A three-sided die gives us a slightly more complex expression. There are now 3^S total possible combinations, but many more than S ways to only roll a single 1. For example, if we get a 1 on the first roll, we can get any combination of 2s and 3s from then on. There are 2^(S-1) such combinations of 2s and 3s, giving us the equation:
P = S * 2^(S-1) / 3^SWe can generalize this to any k-sided die as
P = S * (k-1)^(S-1) / k^Sand voila! Given any probability of life evolving around a star, and the knowledge that there are 10B stars in the Milky Way, we can calculate the odds of humanity being alone.
(Note: I wrote a quick simulation to double-check this formula.)
Interrogating the Formula
Here’s an interesting question: given a certain number of stars S, what value of k maximizes the chances that humanity is alone?
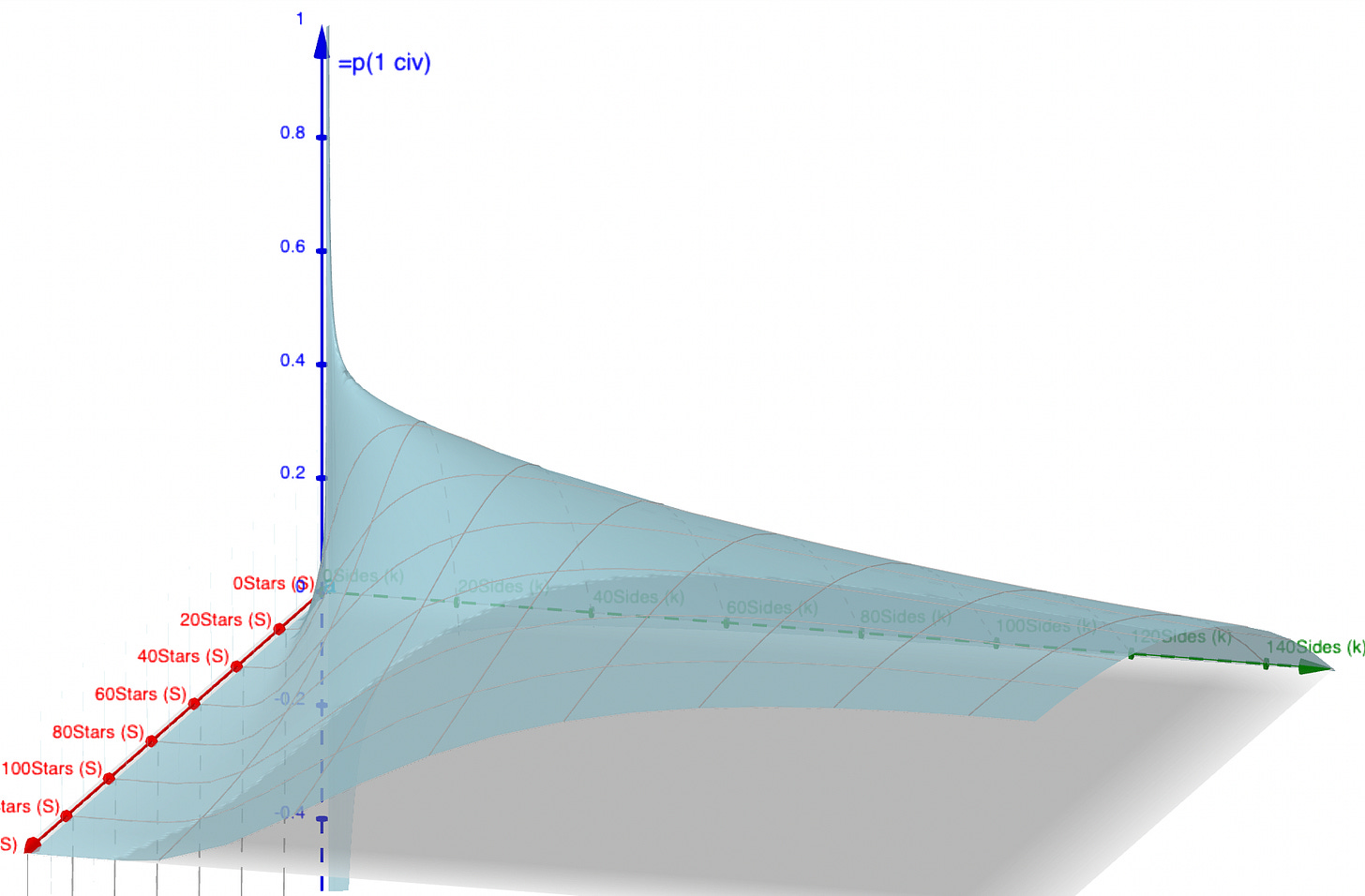
Let’s graph the equation for P as a function of S and k:
We can see a clear maximum along the line S=k, which matches my intuition—you’d want to roll a D20 about 20 times to get exactly one 1. But can we prove this?
First we need to take the derivative of P with respect to k:
P' = S * [k^-S*(S-1)*(k-1)^S-2 - S*k^(-S-1)*(k-1)^(S-1)]Then set it to zero:
0 = k^-S*(S-1)*(k-1)^S-2 - S*k^(-S-1)*(k-1)^(S-1)
k^-S*(S-1)*(k-1)^S-2 = S*k^(-S-1)*(k-1)^(S-1)
(S-1)(k-1)^(S-2) = S * k * (k-1)^(S-1)
S/k = (S-1)/(k-1)
S/(S-1) = k/(k-1)
k = SSo if we have 10B stars, a one-in-ten-billion chance of life forming around a star would maximize the chances of humanity being alone.
But here’s what’s fascinating: with the numbers perfectly fine-tuned, we only have about a 37% chance of being alone! Even if we handicap the odds as much as possible, it’d be more likely than not for humanity to have a sibling.
To put it another way, if you’re going to create a galaxy (or Universe) as big as ours, there’s no way for you to fine-tune the probability of life forming to make it happen exactly once, with any reasonable odds. At most you can get to a roughly one-in-three chance.
To Infinity
You may have noticed from the graph above that our function appears to be converging towards some limit as the number of stars grows. In fact it does, and it’s a pretty elegant one!
First, let’s find the limit when S=k—i.e. the case where the odds of intelligent life emerging are fine-tuned to maximize the chances of only one civilization. I’ll skip the derivation (read: I can’t figure it out) and let WolframAlpha do the work for me:
So with infinitely many stars, and an infinitesimal chance of life forming, we’d expect to see a single civilization about 36.8% of the time. Which is kind of weird to think about.
We can also reformulate our equation a bit to express k as a ratio of S
k = rSSetting r=1 maximizes P, which falls off at higher and lower values for r.
So our equation becomes:
P = S * (rS-1)^(S-1) / (rS)^SA few spot checks on WolframAlpha suggest that, as S goes to infinity, the equation for P as a function of r becomes:
P = 1 / (r * e^(1/r))Here’s what that looks like:
Setting r somewhere between roughly 0.22 and 22—a range of two orders of magnitude—leaves us with at least a 5% chance of life forming exactly once. So there’s still a pretty wide range of values that could feasibly lead to a lonely humanity. But again, any value would on average yield at least one or two siblings.
Caveats
Humanity Could be a Fluke
There’s one major flaw in the reasoning above: we can simply tune the probability of life forming to be extremely low, and count humanity as a fluke. Then we’d almost certainly be alone in the universe.
How much weight should we give to this possibility? Given that we’re here, can we make any assumptions about the probability of life forming, other than it being non-zero?
I’m pretty sure there’s a Bayesian vs Frequentist debate to be had here, but I’d need to spend a lot more time thinking about it.
Existence does not imply Contact
The Drake equation focuses on determining the odds of humanity contacting another civilization. The above just focuses on their hypothetical existence.
If we want to talk about the possibility of contact, we would need to add back in parameters for L (the average lifetime of technological civilizations) and R (the rate of star formation). Wikipedia suggests some other parameters that might be helpful as well.
The Universe is Way Bigger than the Milky Way
There are about as many galaxies in the Universe as there are stars in the Milky Way. So the total number of stars is something like 10^22.
We could make a similar argument to the one above, fine-tuning k or r to maximize the chances of only one civilization appearing in the universe. The same logic would still anticipate two or three civilizations forming, but would almost guarantee that each galaxy would have at most one civilization. Worse, each of those civilizations could follow the logic above to claim that they likely have some siblings in their galaxy!
A lot of the discussion around these numbers gets confusing and contradictory because we only have a single datapoint to extrapolate from. We’ll never come to any firm ground until we either meet aliens, or explore our neighboring stars thoroughly enough to convince ourselves they’re lifeless. Then we could at least start putting some bounds on F. Until then, we can only torture the numbers and listen to their false confessions.
P.S.—Substack, please add MathJax or LaTeX support!